Dioptres sphériques correction d'exercice - Vérifications des connaissances - Optique
On
remarquera que les notations diffèrent de celles utilisées dans le
cours. En effet, l’indice du milieu de la face d’entrée est n et
l’indice du milieu de la face de sortie est n’. La formule de
conjugaison du cours : 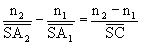 devient
devient 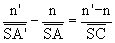 .
.
La vergence est par définition 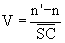 .
.
Sur la figure 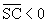 . Le dioptre est convergent si V>0 et donc si n>n’.
. Le dioptre est convergent si V>0 et donc si n>n’.
Le foyer image
est F’ : c’est l’image réelle d’un point à l’infini sur l’axe, c’est à
dire d’un point qui envoie des rayons parallèles à l’axe optique.
Quand les foyers image et objet et le centre d’un dioptre sont donnés on peut tracer 3 rayons connus :
- Le rayon issu de B et parallèle à l’axe optique émerge du dioptre en coupant l’axe optique au foyer image du dioptre.
- Le rayon issu de B passant par le foyer objet du dioptre émerge du dioptre en étant parallèle à l’axe optique.
- Le rayon issu de B et passant par le centre du dioptre émerge du dioptre en ne changeant pas de direction.
Les 3 rayons
tracés se coupent en un même point (conditions de Gauss), ce point est
l’image de B par le dioptre. Un petit objet plan perpendiculaire à l’axe
optique du dioptre donne une image, elle aussi, perpendiculaire à l’axe
optique : l’image de A est donc à l’intersection de l’axe optique et de
sa perpendiculaire passant par B.
Nous nous plaçons
dans le cadre de l’approximation de Gauss ( angles faibles autour de
l’axe optique), nous pouvons sur la figure assimiler la trace de la face
courbe du dioptre à celle de son plan tangent (segment de droite aux 2
brisures indiquant le sens de la courbure).
De plus, le rayon
issu de B passant par S fait un angle par rapport à l’axe optique, ce
rayon émerge du dioptre en passant par le point B’ et en faisant un
angle i’ par rapport à l’axe optique.
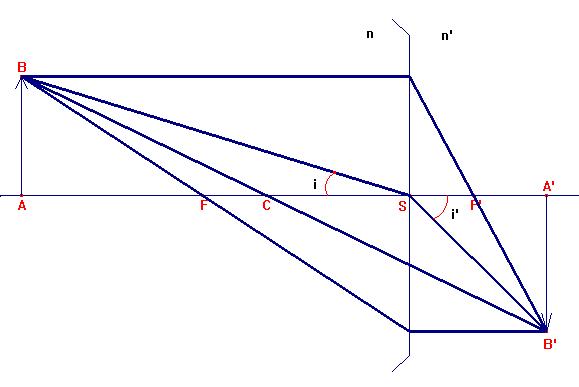
N.B. : Sur la
figure, pour qu’elle soit lisible, on a dilaté les dimensions
perpendiculairement à l’axe optique. Sur cette figure les angles que
forment les rayons avec l’axe optique sont donc beaucoup plus grands
qu’en réalité. On peut donc utiliser les approximations  et
et 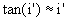 pour le raisonnement.
pour le raisonnement.
Formules de conjugaisons:
Les rayons envoyés sur ledioptre par l’objet A arrivent dans le milieu d’indice n.
Les rayons qui contribuent à la formation de l’image A’ de Aémergent dans le milieu d’indice n’.
- Origine au sommet : 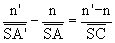
- Origine au centre : 
Formules de grandissement :
- Origine au sommet
comme nous considérons l’approximation de Gauss
donc
De plus grâce aux lois de Descartes, nous pouvons écrire 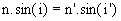 ,
,
mais pour les mêmes raisons :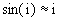 et
et 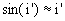 ,
,
nous obtenons donc : .
.
mais pour les mêmes raisons :
nous obtenons donc :
Soit 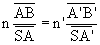 et finalement :
et finalement : 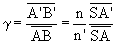
- Origine au centre
D’après le théorème de Thalès dans les triangles CAB et CA’B’, nous pouvons écrire :
- Origine aux foyers
d’après le théorème de Thalès dans les triangles A’B’F’ et F’SI nous pouvons écrire :
d’après le théorème de Thalès dans les triangles ABF et FSJ nous pouvons écrire :
On en déduit la formule de Newton : 
1er Cas :  , l’objet est réel et l’image est réelle.
, l’objet est réel et l’image est réelle.

2ème cas : 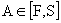 , l’objet est réel, l’image est virtuelle :
, l’objet est réel, l’image est virtuelle :
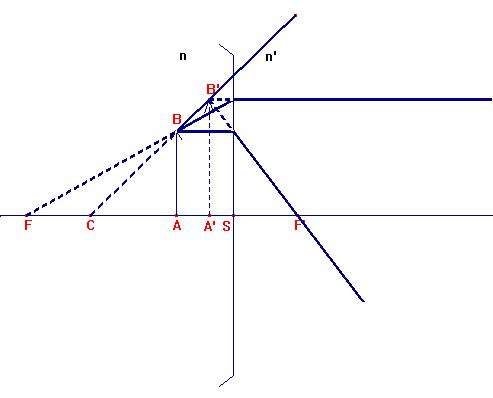
3ème cas :  , l’objet est virtuel, l’image est réelle:
, l’objet est virtuel, l’image est réelle:
Commentaires
Enregistrer un commentaire